Pythonの亀グラフィックス(3)
2019 09 02(art19-0167)
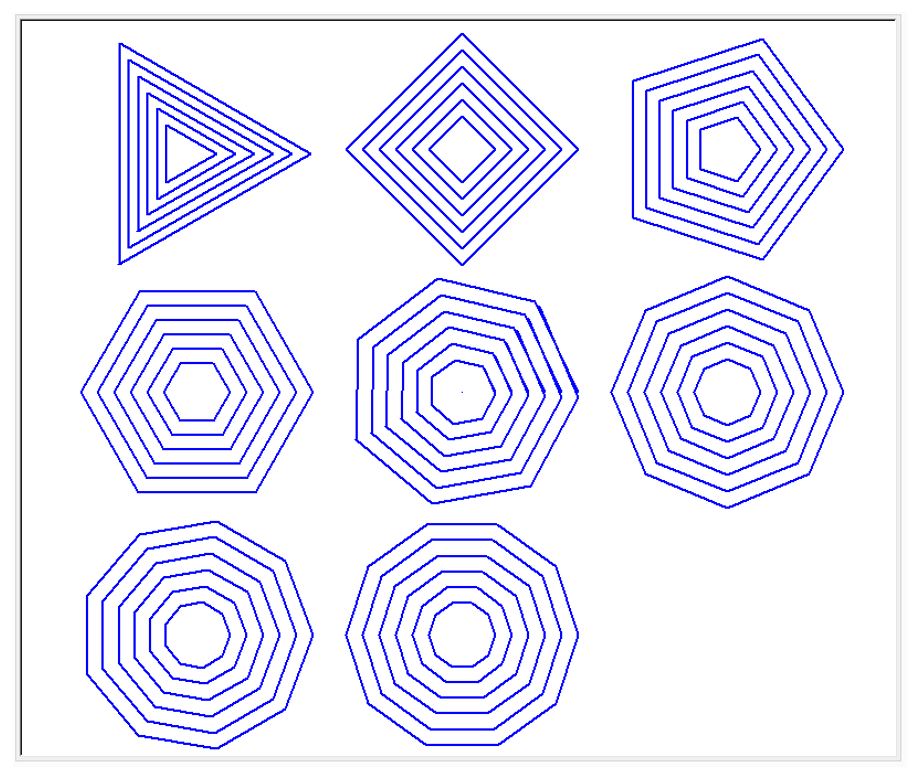
前回、Pythonの亀グラフィックスで描いた図形を紹介しました。円状に並ぶ 24点で、同心円(9個の異なる半径の円からなる)を描かせたものです。なかなか、おもしろい図形になりました。ベースの図形に円を使ったのですが、他の形をつかえばどうなるだろうかと、3 - 10角形を使ってみました。同じ中心をもつ、大きさの異なる正多角形(下図)を、円状に並ぶ 24点に描きました。正多角形の向きは放射線状になるようにしました。
m_triangle.jpg)
_quare.jpg)
.jpg)
.jpg)
正多角形の角数が多くなる(7 - 10角、下図)と、一見同じような模様が出てきますが、よく見ると微妙に違いがあります。 今回は、正多角形の角数だけを、3 - 10と変化させたのですが、他のパラメーター(例えば、同心形同士の間隔、24点の円状配置の広がりなど)を変えれば、同じ、正多角形でも模様が大きく変わります。逆に言えば、描きたい模様があり、それを描かせるパラメーターを知ることは、大変な作業になりそうです。さらに、完成図から、どのように描いたのかを知るすべはあるのでしょうか。このあたり、機械に解けるのか解けないのか、たいへん興味をそそられます。
それにしても、これらの模様、どこかでみたことがあります。それも、非常に身近なものに。思い出しました、ガラス製の皿型の吸い殻入れの模様です。ガラスのカット模様に似ています。今は、使われることなく2階の物置小部屋に収まっています。
.jpg)
.jpg)
.jpg)
.jpg)
