Pythonの亀グラフィックス(3)
2019 09 05(art19-0168)
Pythonの亀グラフィックスを楽しんでいます。亀を動かす指令に、goto()があります。これは、「亀さん、(X、Y) 座標へ移動して」と言うものです。画面上に直交する X軸と Y軸をとると、画面上の任意の点は X値と Y値からなる(X、Y)座標であらわすことができます。亀さんへの指令 goto(X, Y)を使いますと、画面上の任意の点へ亀を移動させることができます。もちろん、けなげな亀は移動しながら線を描いてくれます。
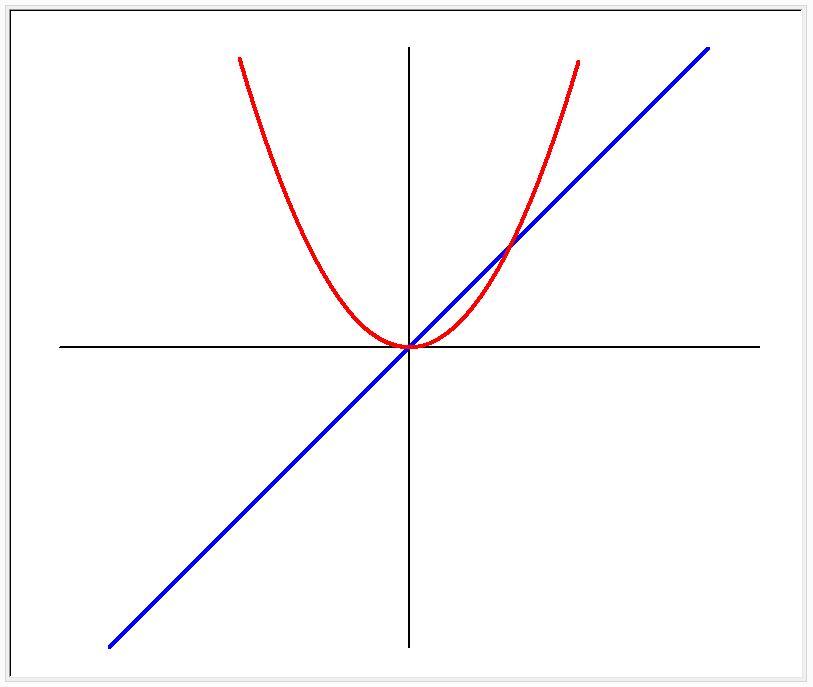
Y値がXによって決定される関数、Y = f (X)は、X-Y座標上に描くことができます。中学で学習した1次関数(Y = X)と2次関数(Y = X^2)は、Xを横軸に、Yを縦軸にとると、下図のように描けます。XとY軸の交点は、(0、0)です。(注:2次関数は、図面からはみ出ないようにY値を1/100に縮小しています)
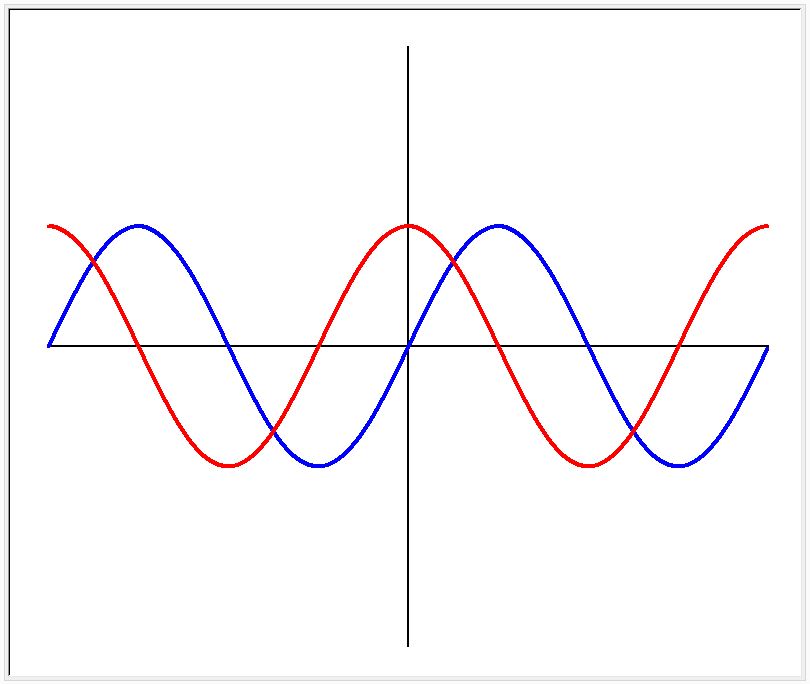
同様に、三角関数、サイン(sin) とコサイン(cos)は、X,Yの関数式、Y = Asin (X) と Y = Acos (X) であらわせます。Xが (-360度) から (360度) へ変化するときの、サイン、コサインの値を(X、Y)座標にプロットすると、下図のような波形になります。青がサインで、赤がコサインです。位相が90度ずれていることが分かります。
2つのサイン、コサインのような波を直角に合わせるとリサージュ波形ができます。波の大きさが同じ場合、両波の周波数(振動数)が同じであれば、リサージュ波形は円になります。(2つの波形の位相のずれによって、円形―楕円形―直線の間で変化します。位相が90度、270度ずれている場合は円形で、0度、180度ずれていると直線になります)。両波の周波数(振動数)が異なっている場合は、少し複雑な波形となります。下図は、周波数(振動数)の比が、1:1 と 1:3 の場合に形成されるリサージュ波形です。
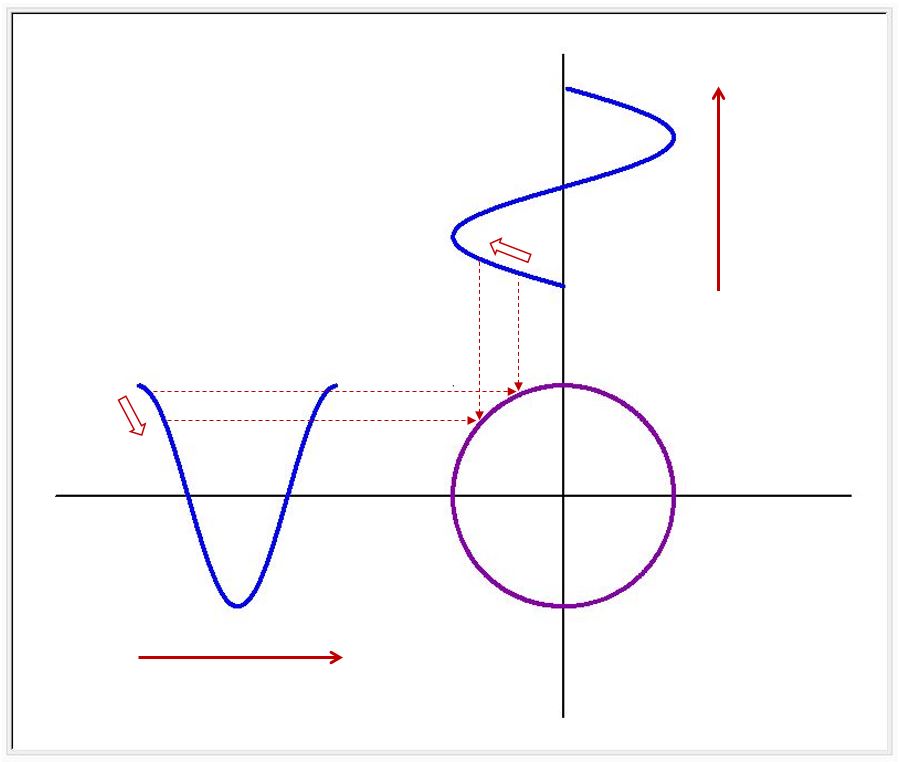
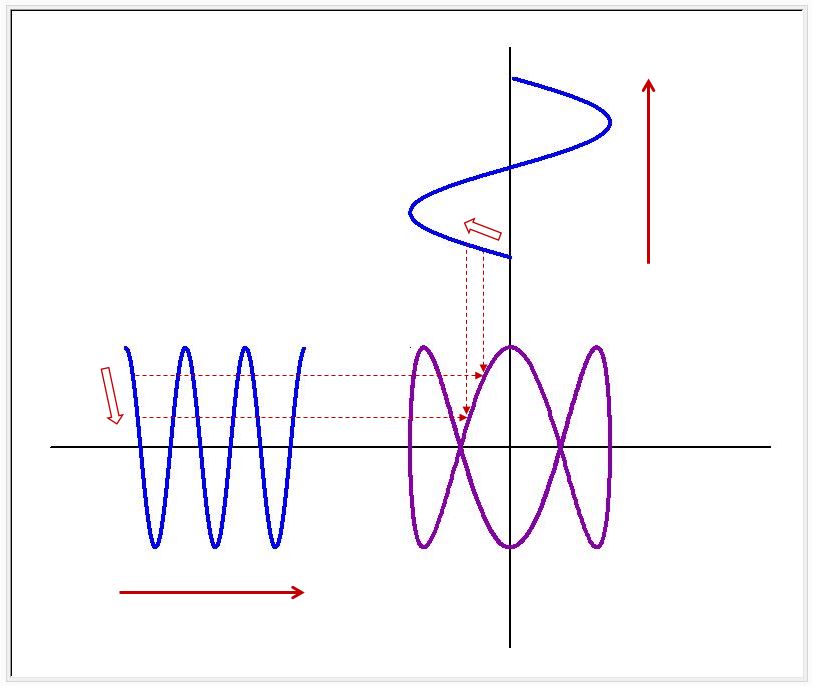
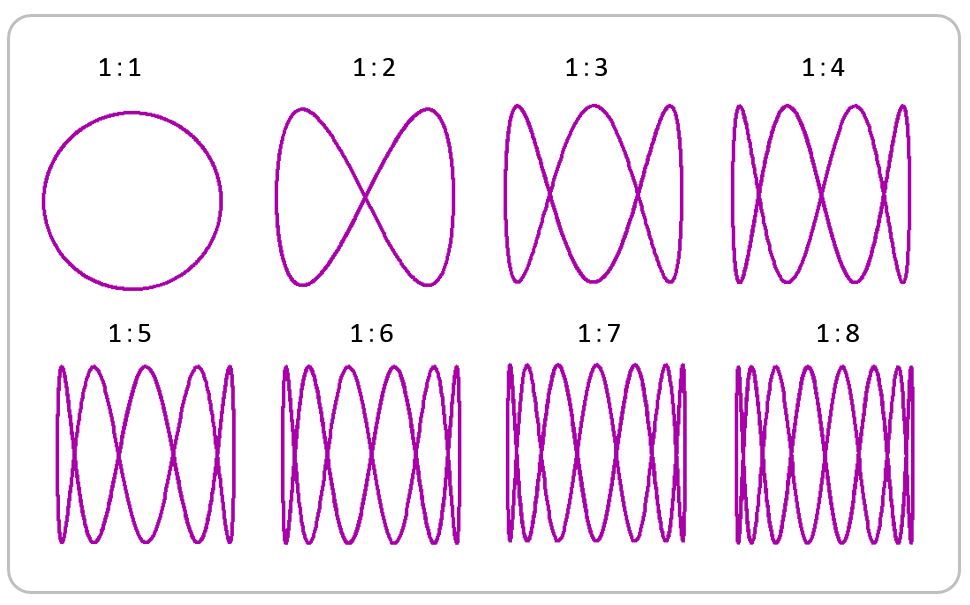
リサージュ波形は、X,Yが時間 t の関数 X (t) と Y (t) としてあらわすことができます。数式は、X = A sin (at + δ) Y = B sin (bt)です。ここで、A、Bは波の大きさ、a:b は周波数比、δ は位相差です。下図に、周波数比を 1:1 から 1:8 へと変化させた時のリサージュ波形を示します。横方向の山の数は1ですが、縦方向の山の数が 1,2,3,4,5,6,7,8 と変化していくことがわかります。
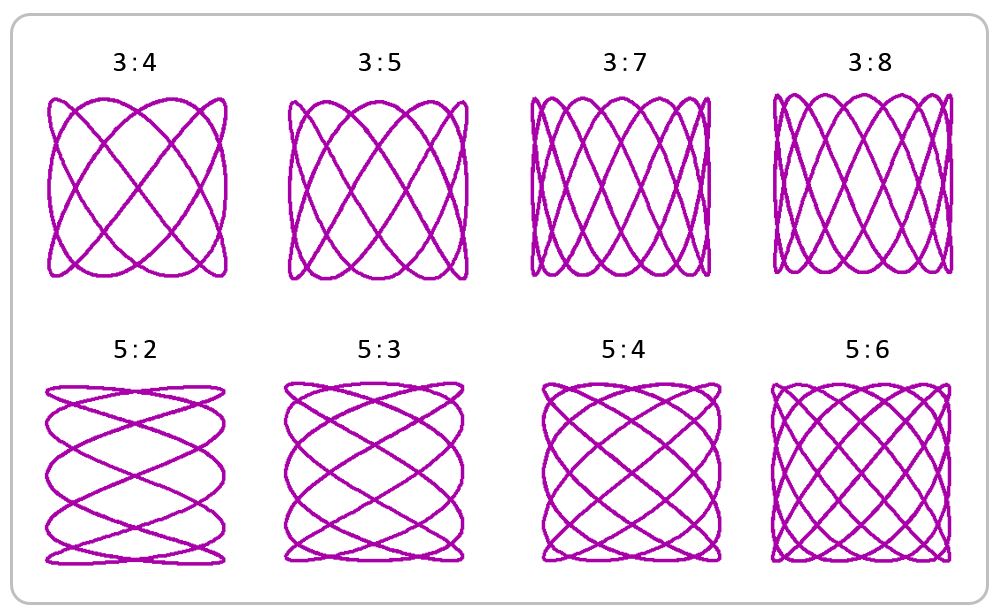
一方、周波数比が複雑(整数倍の関係から外れる)になると、波形も複雑になります。しかし、横山と縦山の数は、3つと4つ、3つと5つなどと、周波数比の 3:4 と 3:5 などに対応していることがわかります(下図)。
このように、両波の周波数比の違いによって、リサージュ波形が異なります。このリサージュ波形の特性を周波数の測定に応用したものが、オシロスコープです。周波数を測定したい波に、周波数が分かっている波を、直交させてリサージュ波形を描きます。リサージュ波形をみながら周波数が分かっている波の周波数を変えていき、リサージュ波形が複雑な波形から単純なものになり、そして円形/直線になるところを探します。この時の周波数が、測定したい波の周波数となります。
米子高専の電気科に在籍していたとき電気測定器機実習がありました。オシロスコープのブラウン管に映しだされる青緑の蛍光色の波形が幾通りにも変化する様は、見ていて飽きないものでした。