Pythonの亀グラフィックス(5)
2019 09 12(art19-0170)
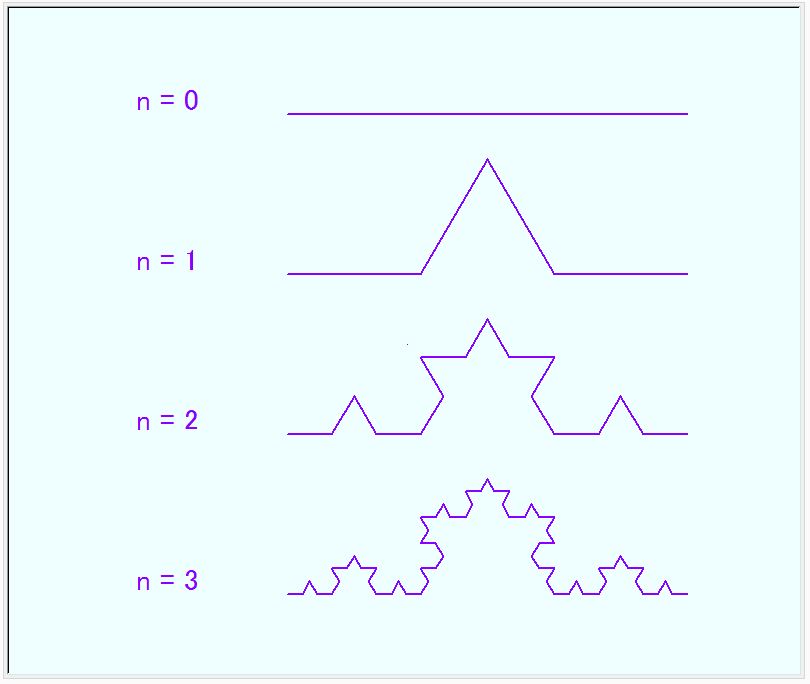
コッホ曲線(Koch curve)と言うフラクタクル図形があります。フラクタクル図形は、図形の部分と全体が自己相似になっているものを言います。相似とは、大きさは異なりますが、形が同じである関係性です。ある図形を拡大、縮小した図形は、元の図形と相似であると言います。コッホ曲線は、3等分された線の中央の線分に、その線分を一辺とする正三角形の2辺が飛び出ている形が繰り返されている図形です。
(n=0): 最初の線はある長さの線です。
(n=1): 3等分された線の中央の線分に、正三角形の2辺が飛び出ます。
(n=2): 4つの線の各々が3等分され、中央の線分に、正三角形の2辺が飛び出ます。
(n=3): 同様に、3等分された各線分の中央に、正三角形の2辺が飛び出ます。
(n=4、5,6・・・): この繰り返しです。
n 数(繰り返し数)を大きくすれは、いくらでも小さな三角形様突起ができますが、あまり小さくてごちゃごちゃしてもつまりませんから、n=3 でとどめ、出来上がったものを繋ぎあわせてみました。

コッホ曲線を描くPython turtleのコードは、あちこちのWebに記載されていますから、それらを参照しながら、書き方を学びました。コードに再帰処理が入りますので多少複雑にみえますが、コンピューターが実際に行う演算・処理の順番をトレースすれば理解が進みます。トレースにはデバック機能が便利です。
さっそく、フラクタクル図形の描画に挑戦してみました。
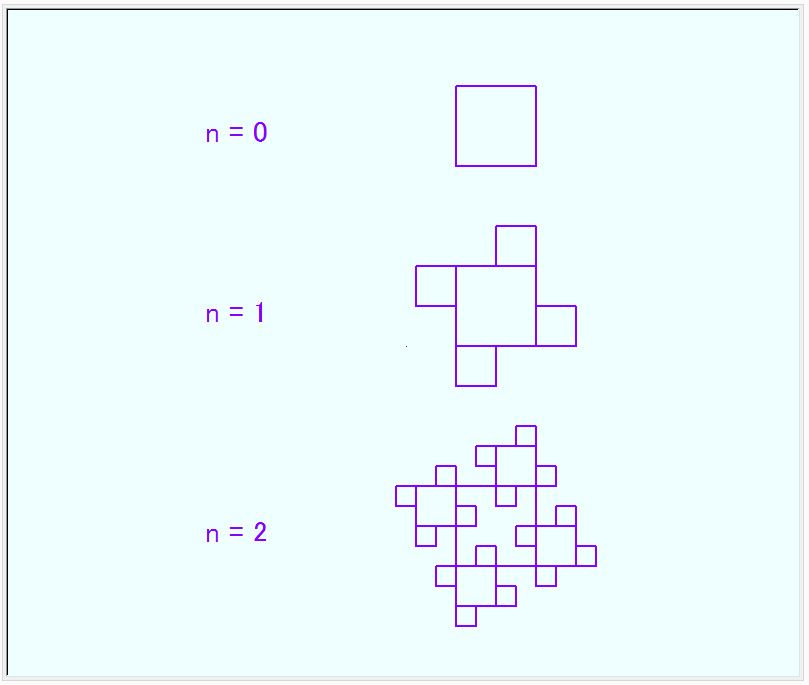
ある正四角形の4隅に、半分サイズの正四角形を付ける。これを繰り返した図形です。何か呼び方があるのでしょうが、ここでは、”4隅四角の四角” としておきましょう。(一応ググってみたのですが、見つかりませんでした)。”4隅四角の四角” の自己相似は、下図の通りです。
(n=0): ある大きさの正四角形。
(n=1):4隅に1/2線分サイズの正四角形が付く。
(n=2): さらに、4隅に1/2線分サイズの正四角形が付く。
(n=3, 4, 5 ・・・): これの繰り返しです。
下の下図は、n=5で、亀さんが描いた ”4隅四角の四角” 図形です。

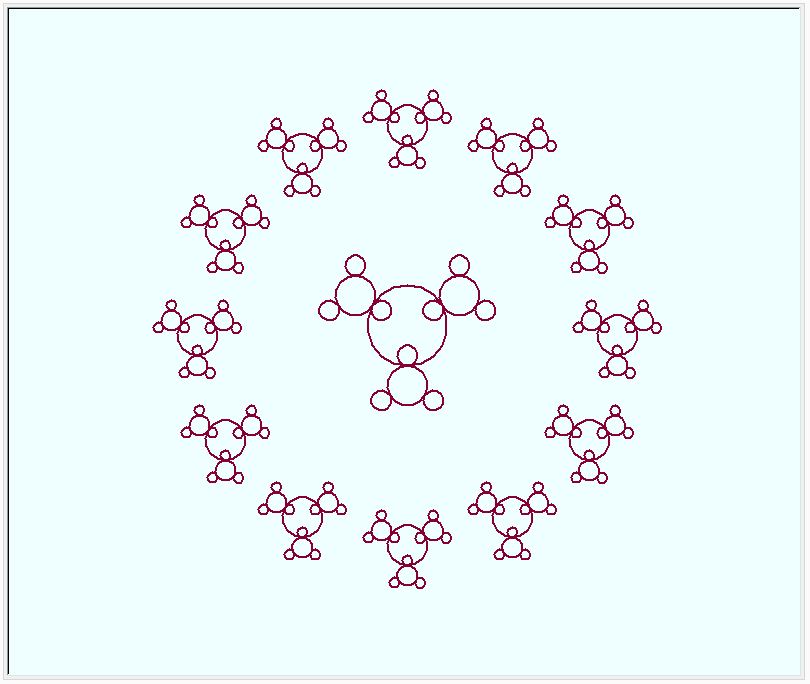
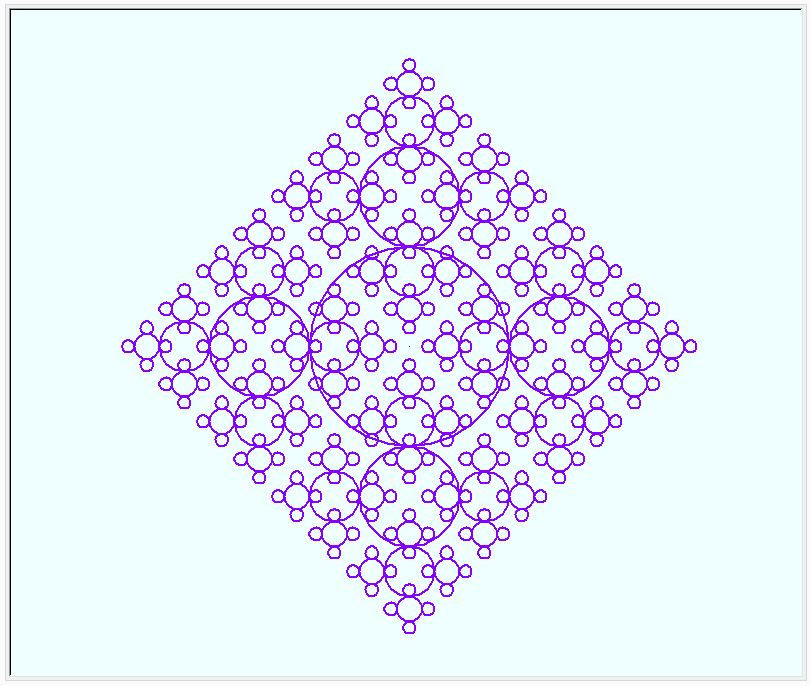
"4隅四角の四角" の正四角形を円に変えてみました。円の4箇所に半分サイズの円を4つ付けたものと、3つ付けたものを描いてみました。名付けて、”4つ円の円” と ”3つ円の円” です。
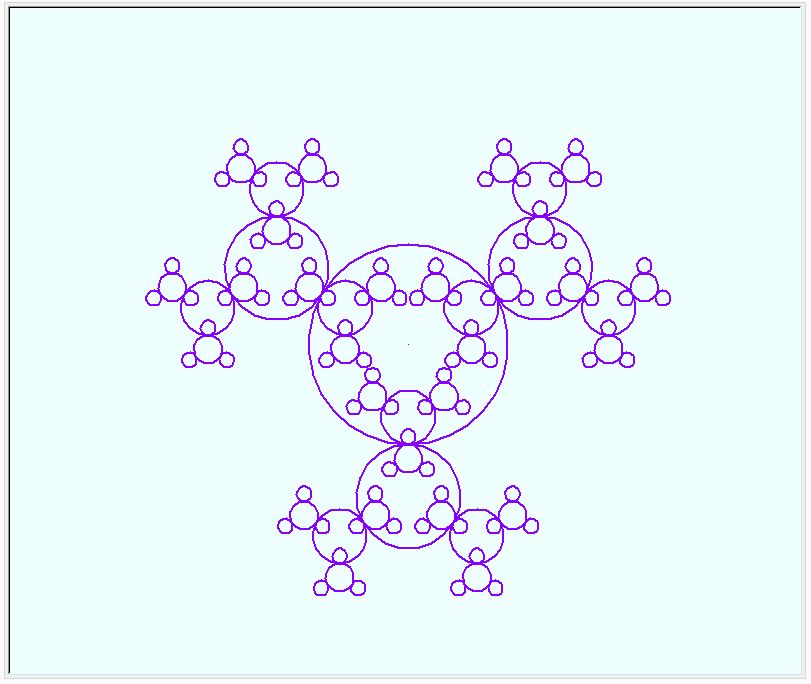
”3つ円の円” の2回繰り返しの形に家内が興味をもちました。何かを連想させるようです。ちょっと、配置を変えてみました。同時に、亀さんに、少し、濃い目のペンで描くように指令しました。出来上がり図形、Tシャツのプリント柄につかえそうです。(既に、出ているような気がしますが?)