新型コロナウイルス感染症(2)
2020 07 30 (art20-0259)
29日、全国の新コロ感染者が千人を超えて、1,264人となりました。東洋経済オンラインによりますと、最近の実効再生産数 Rtは1.3 前後と算出されています(掲載サイトへ)。今現在の Rt 値を出すために、簡易的な計算方法を採用しています。それでも、間違いなく、感染は拡大傾向にあります。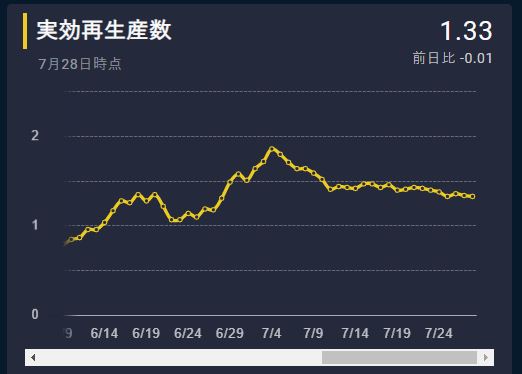
新コロ感染をある程度抑えて、経済活動を維持する。これを実現するためには、外出自粛や人と人との接触・接近を抑える程度を “適切に” 設定する必要があります。これには、これくらい抑えると、感染状況がどうなるといった推定データが役に立ちます。
感染症の数理モデルはいくつかあります。単純なモデルの一つであるSIRモデルを使ってみましょう。ある人が感染すると、数日後に発症し、病原体を放出するようになり周りの人にうつす。その内、回復して (あるいは死亡して) 、病原体を放出しなくなる。SIRモデルでは、感染した人はすぐに病原体を放出し他の人にうつす、とし、病原体の潜伏状態は考えません。
SIRモデルは、人の集団を S, I, R の3つに分類します。
S: Susceptible (感受性保持者、免疫をもたない感染する人)
I : Infectious (感染者、人に感染させる人)
R: Recovered (免疫保持者/回復者、免疫を獲得して感染しない人)
感染症の特徴である感染率と回復率をβとγであらわします。
β:感染率、感受性保持者が単位時間当たりに感染する割合
γ:回復率、感染者が単位時間当たりに回復する割合
S, I, R いずれも時間経過で変化しますからS(t),I(t),R(t)と表記し、数式は以下のとおりです。
dS(t)/dt = -βS(t)I(t)
dI(t)/dt = βS(t)I(t) – γI(t)
dR(t)/dt = γI(t)
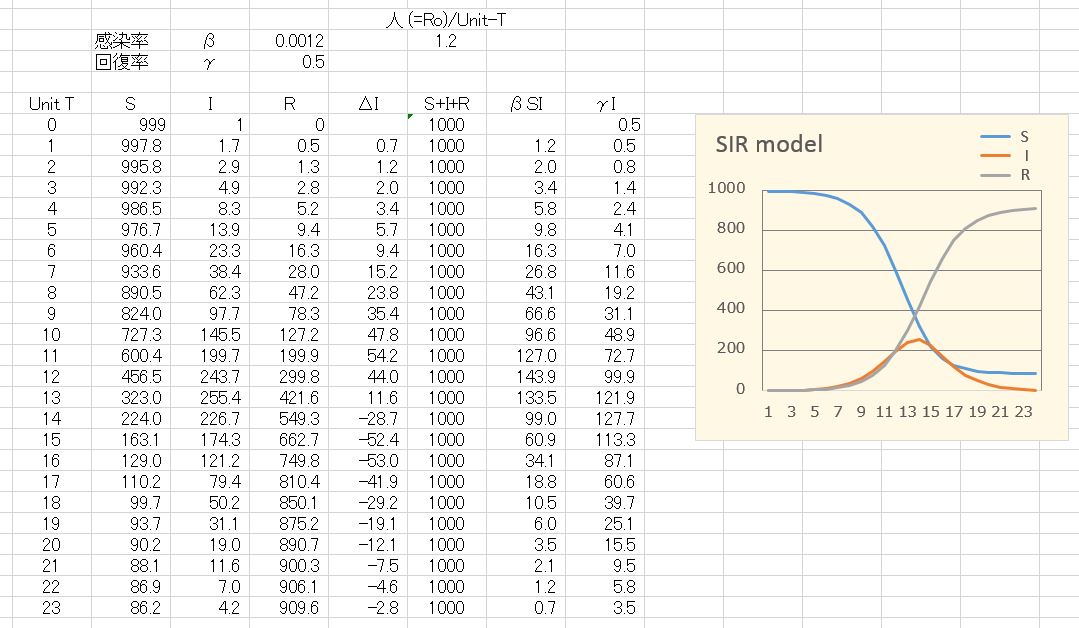
集団の人口を S, I, R の3区分に分けたのですから、S+I+R = constant(定数)になります。この式を加えて、上の微分方程式を解くことができますが、ここでは、各区分の数の変化をみることに意味がありますので、エクセルを用いて、各単位時間点での S, I, R の数値を算出し、その値を時間軸に対してプロットします。
とりあえず、1,000人の集団を考えます。この集団に1人の感染者がいたとします。S=999、I=1, R=0 です。この初期条件で、単位時間当たりの感染率 βを 0.0012, 0.0016, 0.0020と変え、回復率 γを 0.5, 0.8と変えた時の S, I, R の経時変化をプロットしました。感染率 βと回復率 γは、各グラフ図中の上部のかっこ内に (0.0012, 0.5) のように表記しました。
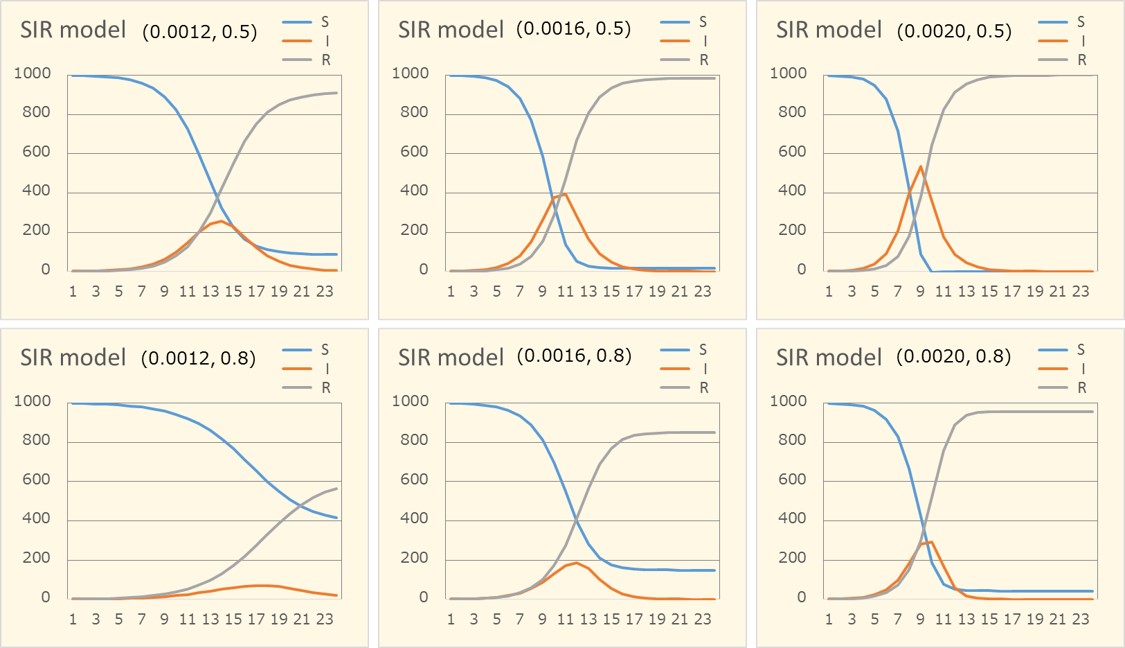
感染者数 I(赤ペン)の変動に注目すると、β と γ の値を変えることで、感染者数のピークの高さと時間点が変わります。感染率 βが下がると、あるいは、回復率 γ が上がると、感染者数のピークが低くなり、ピークの出現が遅れることが読み取れます。
逆に言えば、感染者数のピークを低くし、出現を遅らせるには、感染率 βを下げるか、回復率 γを上げればよいことが分かります。実際、我々が行っている、外出自粛、人と人の接触・近接の距離(社会的距離)を大きくとること、飛沫防止用マスクを装着することなどは、β を下げています。また、感染者をホテルや療養施設や病院に隔離することも、β を下げることになります。また、手厚い治療体制の完備は、γ を上げることに繋がります。感染のピークを下げて、その出現を遅らせるには、我々が今日行っていることを、どの程度やればよいのかを知ることができます。感染症の数理モデルが活用されている理由です。
実際の感染症は、SIRモデルで考えた感染過程のような単純なものではありませんので、もっと、多数の因子(例えば、病原体が感染し発症するまでの潜伏期間)を入れたモデルを用いて解析することになります。

