Pythonの亀グラフィックス(6)
2019 09 26 (art19-0174)
フラクタクル (art19-0170) を含め、幾何学図形はなかなか面白いものです。3つの楽しみ方があります。(1)Web検索などで、探し出した図形を眺めること。
(2)どうやって亀に描かせるのか考え、それ用のプログラムを書くこと。
(3)亀が画面上を動きまわって、少しずつ図形を描くのを眺めること。
Web検索で目にした図形を描いてみました。いずれも、ありふれたものです。
ヒルベルト曲線(Hilbert curve, 左上)
レビーC曲線(Levy C curve、右上)
ドラゴン曲線(Dragon curve、左下)
T正方形 (T-squares、左下)

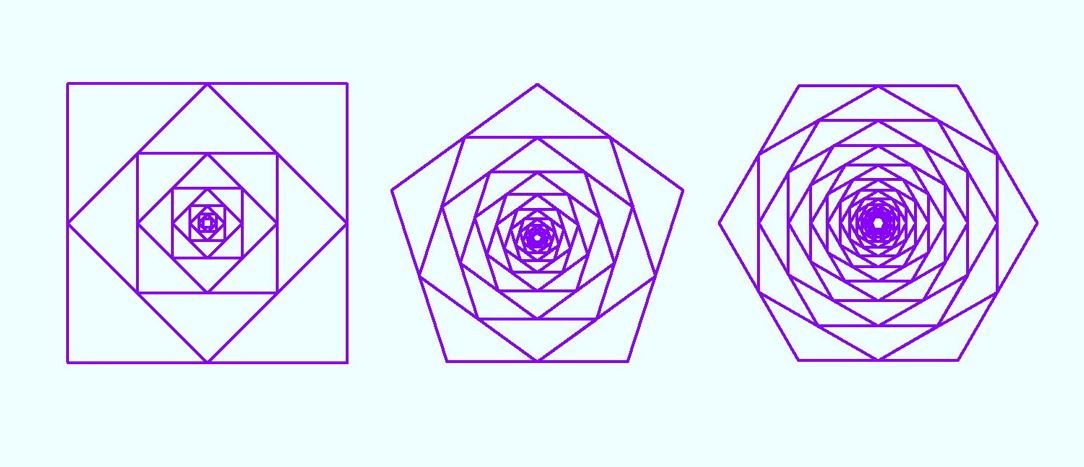
また、単純な図形として、正4, 5, 6角形の内側に同じ正角形を持っている図形を描いてみました。とても単純な描画ですが、ちょっと見には、花に見えます。
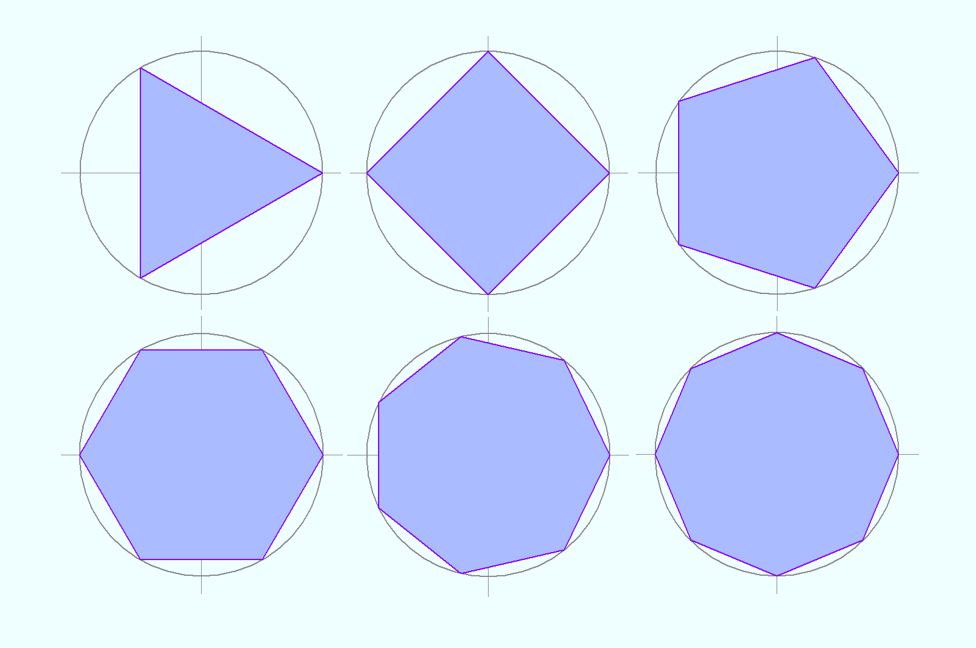
xy座標上に、(0, 0) を中心とした半径Aの円があるとき、円周上の任意の点 (x, y) は、x軸との中心角をθとすると、x = A cosθ、y = A sinθで表すことができます。ここでθは0 - 360度です。θを飛び飛び、例えば、90度ごと (0, 90, 180, 270, (360)) に取り、直線でつなげば、正4角形ができます。飛び飛びの大きさを変えて、正3 - 8角形を描いてみました。7角形だけがちょっと不安です。見慣れないせいでしょうか。前に、筆立てを作ったときと同じような感覚です (art19-0103 と art19-0106)。
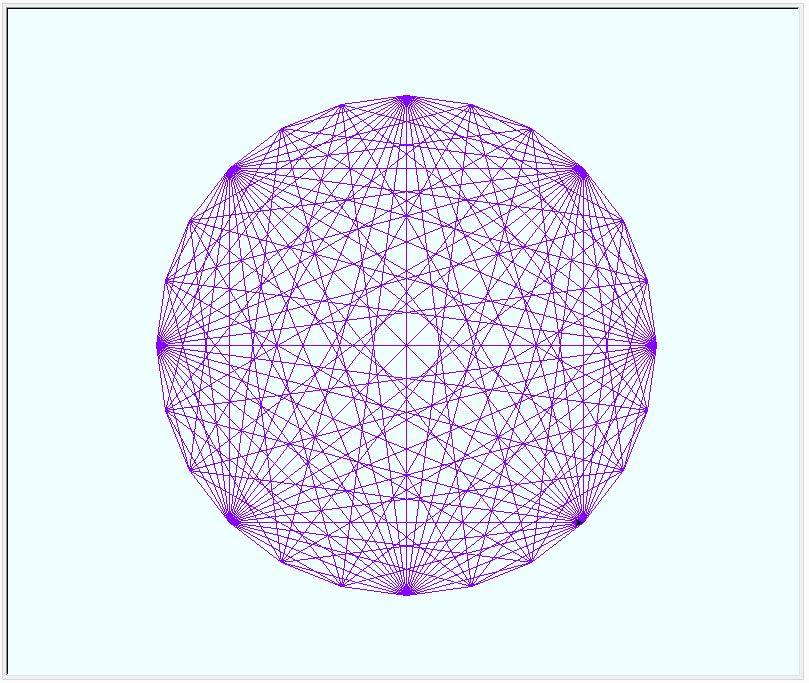
さて、正多角形の各頂点同士を直線で結んでみました。頂点の数が少ないとものたりませんから、頂点の数を増やしました。ただし、増やし過ぎは煩雑になりますから、24頂点の正24角形としました。下図は、単純に頂点同士を結んだだけですが、少しは眺めるに値するようです。結ぶ線の数を減らすと、少し、軽くなりました。