区民運動会 (第42回)
2019 09 30 (art19-0175)
空模様に懸念がありましたが、29日、区民運動会が東郷池の湖岸公園の催し広場で開催されました。区民運動会は班対抗の運動会です。広場の中央に、周辺300m程度のトラックが白い石灰でひかれ、それを取り囲むように、各班のテントが立ちました。
定刻の9時になると、参加区民が中央に集合しました。開会式が執り行われた後、ラジオ体操第一のリズムに合わせて体をほぐしました。凡夫にとって、久しぶりのラジオ体操でした。歳をとったせいでしょうか、テンポが合いませんでした。
運動会は班対抗です。多人数の班もあれば、少人数の班もあります。凡夫の斑(北部3班)は小さな斑ですから、ふさわしい人を選ぶ(選手)ことはどだい無理です。出場選手リストには、凡夫を含めた数名は、上手下手を問わず、全ての種目にエントリーされています。また、我が斑唯一の大所帯のS家の家族は、3世帯でのエントリーとなっています。ご苦労さまです。
凡夫の参加した競技種目は以下の通りです。
最初に出場した競技は、「飲食リレー」です。アンパン => ラムネ => バナナ => ちくわ => ビールと5名で食べ繋いでいきます。凡夫は、第一走者として、アンパン喰いを担当しました。はやく食べる(正確には、ほおばる)ことができず、大差のビリで次の走者にバトンを渡すことになってしまいました。この遅れが最後まで影響しました。のっけから、やる気を損なうことになり、穴にでも入りたくなります。
次の競技は、男女4名ずつの総数8名による「綱引き」です。20秒1本勝負。これは、相手が剛力斑で完敗でした。
「250歳リレー」は、走者8名の合計が250歳以上であることが条件です。急遽かりだされた小学生と中学生がよく走ったのですが、いかんせん、その他が、ふがいなく、結果はほぼビリでした。凡夫は、ジョギングを続けているので、すこしは走れると考えていましたが、大きな錯誤でした。
昼食。斑のテント下で、輪になって、持ち寄った昼食を食べました。
午後の競技の前に、「はわい音頭」の曲が会場に流れました。食事後の雑談に興じていた多数の人が立ち上がり、中央に大きな輪をつくり踊りを披露しました。凡夫の家内も加わり、見よう見まねで踊っていました。しかし、曲が「浅津小唄」(art18-0086) に変わると、大きな人の輪は崩れ、数人の小さな輪となりました。この踊りを、意識してみたのは初めてです。大衆受けしそうにない踊りで、楽しく踊れる、あるいは、踊っていて楽しい、ことから外れているような印象をうけました。
午後の競技種目は、「満水リレー」でした。バケツの水を湯飲みに入れて運び、一升瓶に注いで満杯にする競技です。早く走ることだけでなく、水をこぼさないで運ぶこと、運んだ水をできるだけ一升瓶に入れることが問われます。走るだけでは済まないこの競技、ほぼ全員参加の我が斑は、みごと、1着でした。喜びのハイタッチ。しかし、この1着、良かったのか悪かったのか。これで、総合得点でのブービー賞をのがしたのかもしれません。しかし、どうも、競技となると、老若男女を問わず向きになってしまうものです。そう、やめられない、とまらない、です。
全ての競技が無事に終わりました。閉会式では優勝班の表彰がありましたが、我が斑には縁の無いことです。そして、参加者は、後片付けを済ませて、三々五々家路につきました。皆さん、お疲れ様でした。
Pythonの亀グラフィックス(6)
2019 09 26 (art19-0174)
フラクタクル (art19-0170) を含め、幾何学図形はなかなか面白いものです。3つの楽しみ方があります。
(1)Web検索などで、探し出した図形を眺めること。
(2)どうやって亀に描かせるのか考え、それ用のプログラムを書くこと。
(3)亀が画面上を動きまわって、少しずつ図形を描くのを眺めること。
Web検索で目にした図形を描いてみました。いずれも、ありふれたものです。
ヒルベルト曲線(Hilbert curve, 左上)
レビーC曲線(Levy C curve、右上)
ドラゴン曲線(Dragon curve、左下)
T正方形 (T-squares、左下)
また、単純な図形として、正4, 5, 6角形の内側に同じ正角形を持っている図形を描いてみました。とても単純な描画ですが、ちょっと見には、花に見えます。
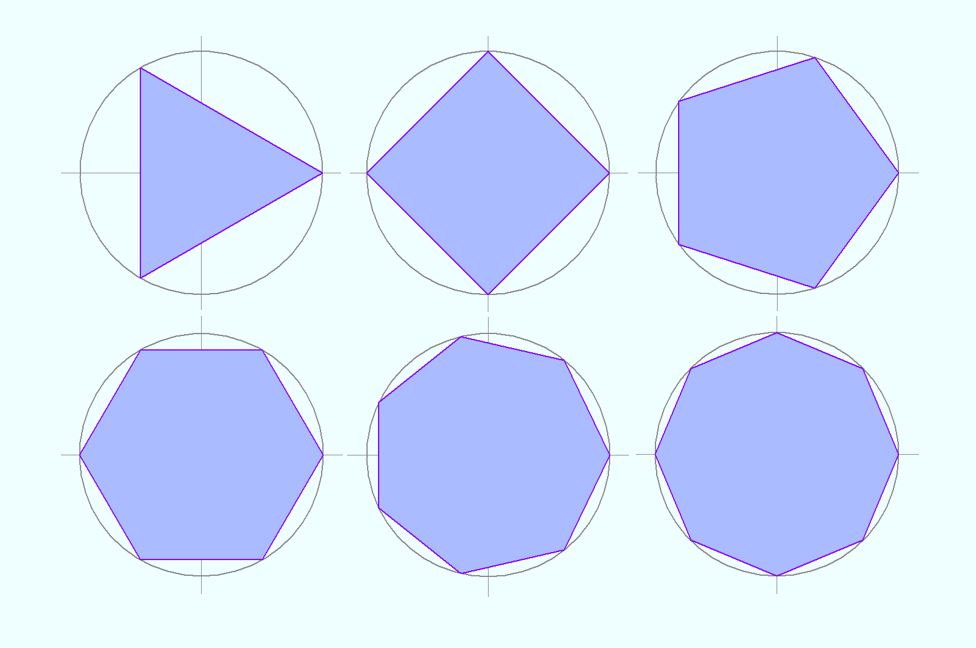
xy座標上に、(0, 0) を中心とした半径Aの円があるとき、円周上の任意の点 (x, y) は、x軸との中心角をθとすると、x = A cosθ、y = A sinθで表すことができます。ここでθは0 - 360度です。θを飛び飛び、例えば、90度ごと (0, 90, 180, 270, (360)) に取り、直線でつなげば、正4角形ができます。飛び飛びの大きさを変えて、正3 - 8角形を描いてみました。7角形だけがちょっと不安です。見慣れないせいでしょうか。前に、筆立てを作ったときと同じような感覚です (art19-0103 と art19-0106)。
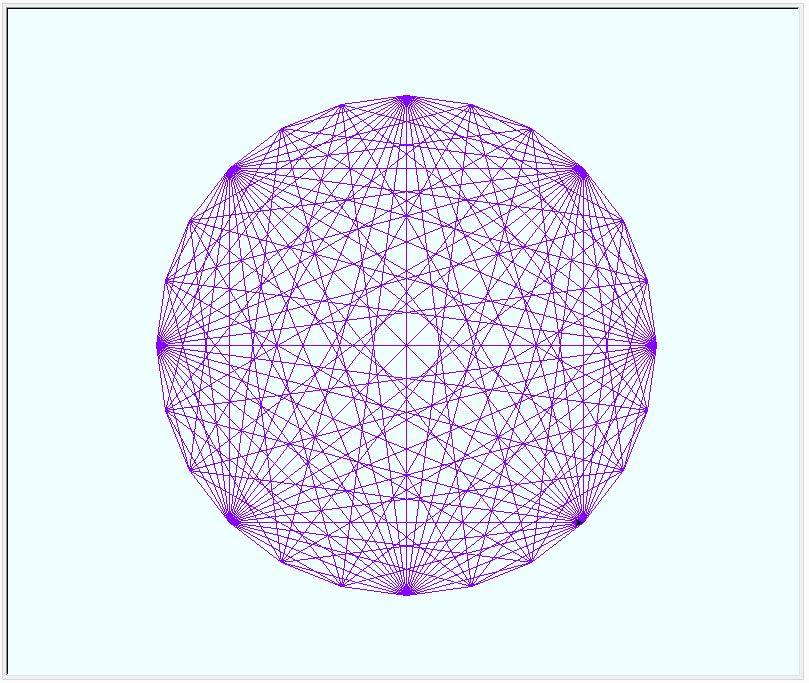
さて、正多角形の各頂点同士を直線で結んでみました。頂点の数が少ないとものたりませんから、頂点の数を増やしました。ただし、増やし過ぎは煩雑になりますから、24頂点の正24角形としました。下図は、単純に頂点同士を結んだだけですが、少しは眺めるに値するようです。結ぶ線の数を減らすと、少し、軽くなりました。
夏野菜の虫(幼虫)
2019 09 23(art19-0173)
夏野菜の栽培には虫がつきものです。
いろいろな虫がやって来ては葉や実を食べます。
キュウリの葉には、小型の甲虫、ウリハムシの姿をよく見かけます (art18-0024)。捕獲しようと手を伸ばすと、ぽとりと落ちます。地面に落ちるのではなく、落下途中の葉にしがみつくか、飛翔して横方向へ逃げます。この習性がわかれば捕獲するのは簡単です。虫の下方から網をいれて、虫を上方からつつけば、網の中に落ちてきます。昨年学習したことが役立っています。
今年はキュウリを長い期間栽培したせいか、ウリノメイガの幼虫を見かける機会が多々ありました。幼虫の体色はツヤツヤした緑色で、背中に2本の白い筋が通っています。キュウリの葉の端が所々巻いています。開くと中に幼虫が潜んでいます。また、葉の表面に、ゴマ粒より少し細かい黒褐色の糞が多数付いていることがあります。上方の葉を調べるとウリノメイガの幼虫がいます。糞の量から、さぞかし大きな幼虫だろうなと思いますが、見つかる幼虫は小さく、ちょっとした違和感が残ります。
キュウリとカボチャの葉に、ウリキンウワバの幼虫を見かけました。体色は緑色で、背中に2本の白い筋があり、多数の突起がついています。体を折り曲げた姿は、異様です。それは、尺取虫のように、体を屈伸させて移動することに因があります。大き目の幼虫ですから、硬い葉も難なく摂食します。
ナスの果実にヨトウムシの幼虫がいました。まだ若齢の幼虫です。体色は茶褐色で、背中線に黄色の線が通っています。もっぱら葉を食用としていますが、果実も食べるようで、ナスの果皮が齧られています。
トマトの果実が落下するようになりました。拾ってみると穴があいています。枝に付いている果実の幾つかにも穴があいています。多くは1ミリ径の穴ですが、なかには、数ミリ径の穴も見られます。大きな穴に、薄黄色のオオタバコガの幼虫がいました。大食家らしく、穴の周りを排泄物だらけにしています。また、別のトマトには、緑色の幼虫がいました。こちらは、穴を開けることなく、表面を広く齧っています。こちらも、大食いのようです。
夏の果樹と収穫(2019年)
2019 09 19(art19-0172)
プルーンを収穫しました。8月になると果皮が緑色から赤褐色に変化し始めました。お盆を過ぎる頃に深紫色に変わりました。どんな按配かと、一つ果実をもぎ取って齧ってみました。硬く、しかも酸味が強く食べられたものではありませんでした。まだまだのようです。果実をながめては ”食べごろ” をはかっていました。8月末になると、木の周りに落果を見かけるようになりました。拾ってみると、鳥がつついた跡や、虫の幼虫が食べた跡(果柄と接する周辺部)があります。木に生っているプルーンの果実の幾つかにも同様な跡が見られました。鳥がつつき、虫の幼虫が食べるようになったのですから、そろそろ、”食べごろ” になっていると思われます。9月に入って数日後、プルーンの実を食べてみると、柔らかく、プルーン独特の甘みがありました。”食べごろ” を迎えています。さっそく、2回にわけて収穫しました。総数50個ほどのプルーンです。
プルーンの木は、畑のなかでは、一番大きな木です。しかも、2本。50個ほどしか収穫できないとは、なんとも、なさけないことです。
冬の1月、花芽を残すように、自分なりに剪定を試みたのです(art19-0098)が、良くなかったようです。着花数が少なく、また、花の付き方にむらがありました。一部の枝にだけ花がついている状態でした。全ての枝に、花を沢山、満遍なく咲かせるにはどうしたらよのか、難しい問です。大きな課題となりました。一度、樹形を変える程の大胆な整形をやってみようかと考えています。
もう一つの夏の果実、イチジク。収穫完了です。期間は、8月14日から9月13日の一ヶ月間。13日に9個を収穫して、今年のイチジクは終わりました。総数88個です。このイチジクは早生で、近所のイチジクより、随分早く実が熟します。その分、早く終わってしまいます。
今年は家内がイチジクでジャムを作りました。形容こそ変わっていますが、当分、自家製イチジクを味わうことができます。
夏野菜の栽培と収穫(2019年)
2019 09 16(art19-0171)
今年も4種類の夏野菜を栽培してきました。14日、冬野菜 (ダイコン) の栽培スペースをつくるため、キュウリ、トマト、ナスの全株を処分し、整地しました。西側の1畝に植わっているピーマンとパプリカの株は残しています。
夏野菜の収穫総数をまとめてみました。
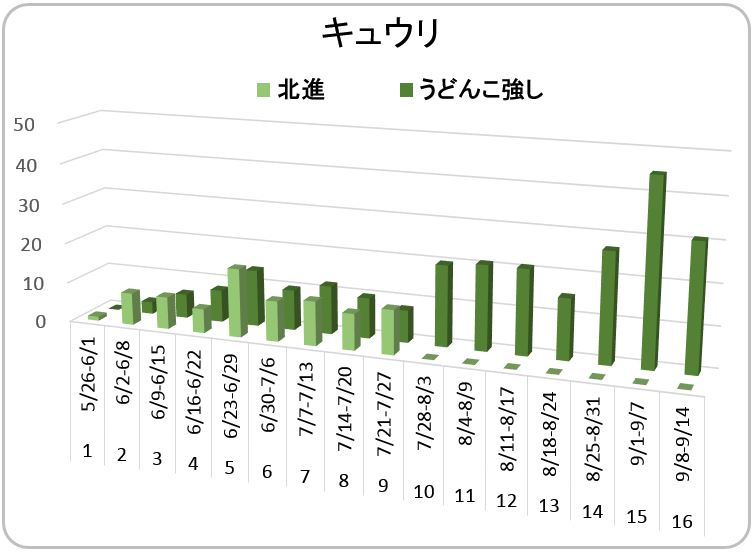
【キュウリ】
北進(2株)(7/19まで) 81本
うどんこ強し(2株) 251本
キュウリは、2品種栽培しました。"北進" は、7月の低温と降雨続きの悪天後、うどんこ病に罹りました。実がついていましたので薬剤を散布しないで、罹患葉を摘取したのですが、病気の進行を止めることができませんでした。止む無く引き抜いて処分しました。一方、"うどんこ強し" は病気に罹ることなく、悪天を耐え抜けました。その後も、成長を続けながら、開花―着果―肥大を繰り返しました。先日 (14日) 、栽培スペース確保の都合上、処分しましたが、残しておけばまだまだ収穫できそうでした。すこし、残念です。しかし、2株で251個の果実が取れましたから、もう十分です。
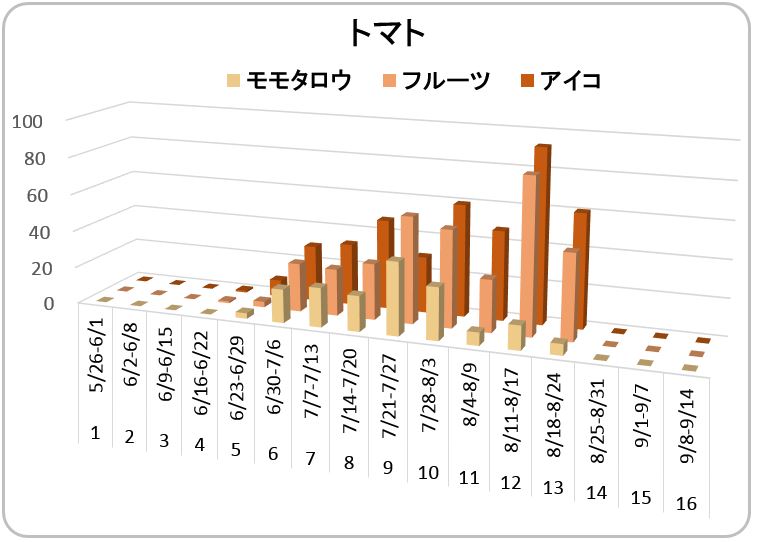
【トマト】
モモタロウ(4株)154個
フルーツ(2株) 351個
アイコ(2株) 413個
3品種とも摘心をしないで栽培しました。”モモタロウ” は、上位葉にも花をつけるのですが着果率が低く、着果しても花房がなかなか大きくなりませでした。そのため、収穫できた期間が短く、ほぼ7月の一ヶ月間でした。一方、”フルーツ” と ”アイコ” の両品種は、上部の葉の成長に伴い、次々と開花ー着果ー肥大が繰り返され、長い期間収穫できました。また、”フルーツ” と ”アイコ” は、小型のトマトであり、成熟までの時間が短く、その分数多く取れました。8月下旬になると、変形果が出てくるようになりました。果皮が硬くなり、虫食い果が多くなりましたので、収穫は控えました。
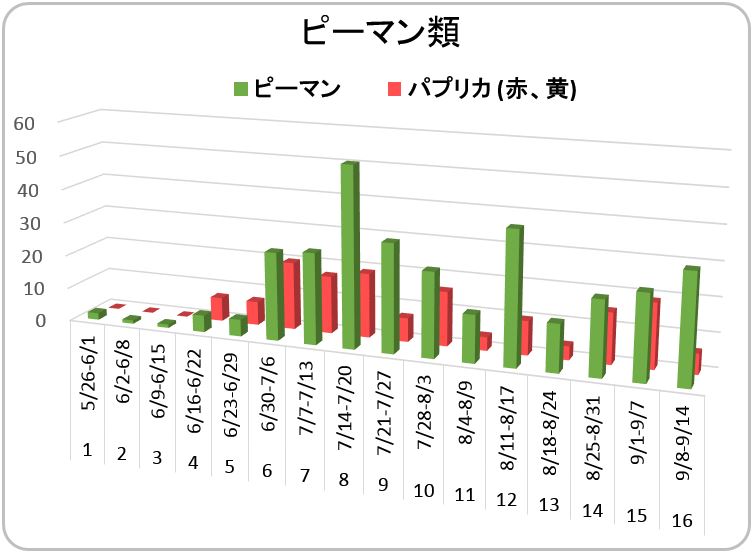
【ピーマン類】
京みどり、エース(各2株) 323個
パプリカ(赤、黄 各2株) 151個
ピーマンとパプリカは、一度、花をつけると、次々と開花し、着果・結実・肥大を続けます。14日時点で、まだまだ、株に勢いがありました。これからも、多数の実をつけてくれると思います。
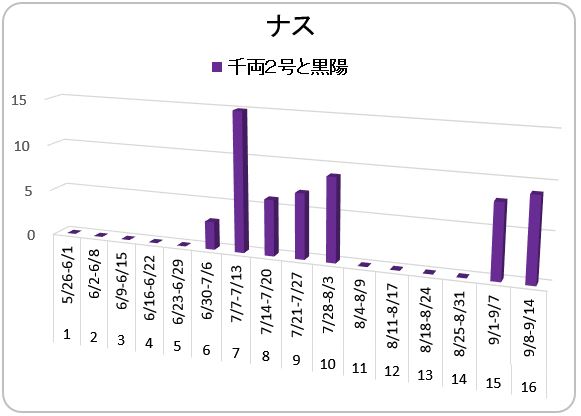
【ナス】
千両2号、黒陽(各2株) 57本
昨年同様、今年も、ナスの栽培はうまくいきませんでした。苗の定植後の生育が悪かったこと (art19-0150) が、尾を引いたのではと思っています。
Pythonの亀グラフィックス(5)
2019 09 12(art19-0170)
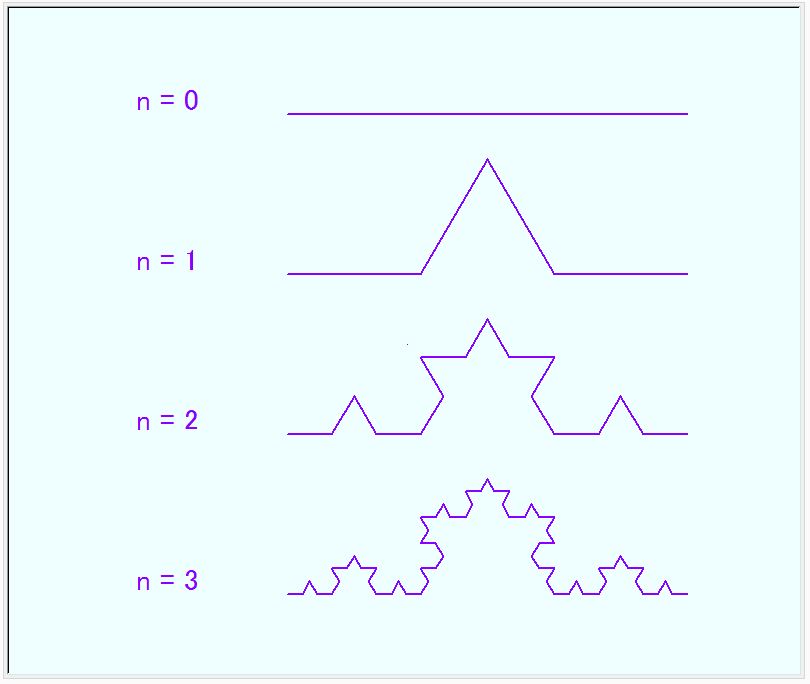
コッホ曲線(Koch curve)と言うフラクタクル図形があります。フラクタクル図形は、図形の部分と全体が自己相似になっているものを言います。相似とは、大きさは異なりますが、形が同じである関係性です。ある図形を拡大、縮小した図形は、元の図形と相似であると言います。
コッホ曲線は、3等分された線の中央の線分に、その線分を一辺とする正三角形の2辺が飛び出ている形が繰り返されている図形です。
(n=0): 最初の線はある長さの線です。
(n=1): 3等分された線の中央の線分に、正三角形の2辺が飛び出ます。
(n=2): 4つの線の各々が3等分され、中央の線分に、正三角形の2辺が飛び出ます。
(n=3): 同様に、3等分された各線分の中央に、正三角形の2辺が飛び出ます。
(n=4、5,6・・・): この繰り返しです。
n 数(繰り返し数)を大きくすれは、いくらでも小さな三角形様突起ができますが、あまり小さくてごちゃごちゃしてもつまりませんから、n=3 でとどめ、出来上がったものを繋ぎあわせてみました。
コッホ曲線を描くPython turtleのコードは、あちこちのWebに記載されていますから、それらを参照しながら、書き方を学びました。コードに再帰処理が入りますので多少複雑にみえますが、コンピューターが実際に行う演算・処理の順番をトレースすれば理解が進みます。トレースにはデバック機能が便利です。
さっそく、フラクタクル図形の描画に挑戦してみました。
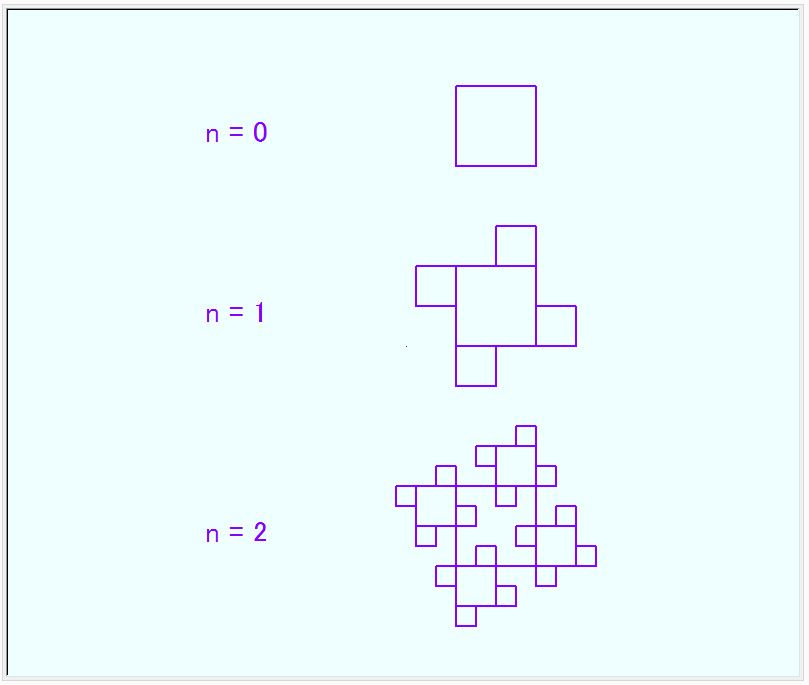
ある正四角形の4隅に、半分サイズの正四角形を付ける。これを繰り返した図形です。何か呼び方があるのでしょうが、ここでは、”4隅四角の四角” としておきましょう。(一応ググってみたのですが、見つかりませんでした)。”4隅四角の四角” の自己相似は、下図の通りです。
(n=0): ある大きさの正四角形。
(n=1):4隅に1/2線分サイズの正四角形が付く。
(n=2): さらに、4隅に1/2線分サイズの正四角形が付く。
(n=3, 4, 5 ・・・): これの繰り返しです。
下の下図は、n=5で、亀さんが描いた ”4隅四角の四角” 図形です。
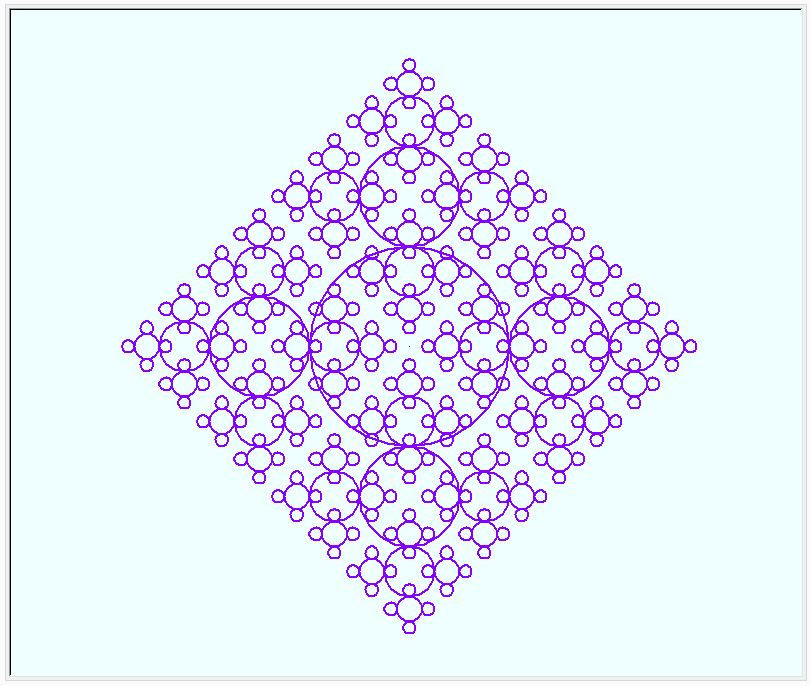
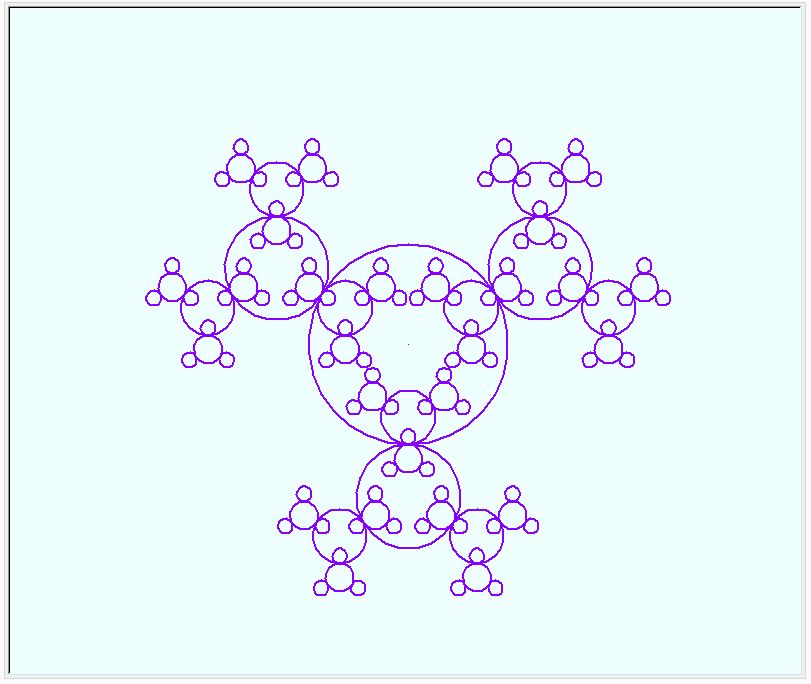
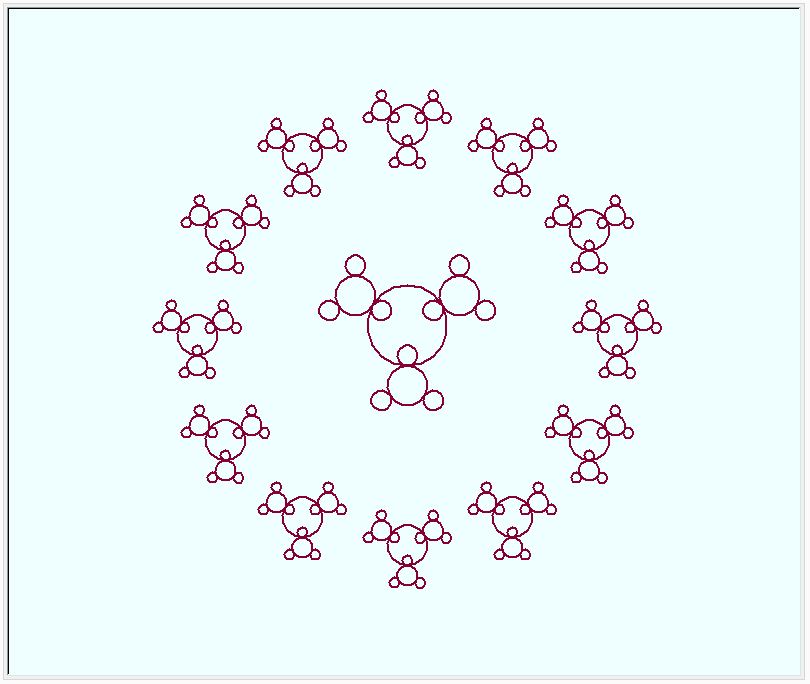
"4隅四角の四角" の正四角形を円に変えてみました。円の4箇所に半分サイズの円を4つ付けたものと、3つ付けたものを描いてみました。名付けて、”4つ円の円” と ”3つ円の円” です。
”3つ円の円” の2回繰り返しの形に家内が興味をもちました。何かを連想させるようです。ちょっと、配置を変えてみました。同時に、亀さんに、少し、濃い目のペンで描くように指令しました。出来上がり図形、Tシャツのプリント柄につかえそうです。(既に、出ているような気がしますが?)
Pythonの亀グラフィックス(4)
2019 09 09(art19-0169)
今日も、亀さんに活躍していただきます。
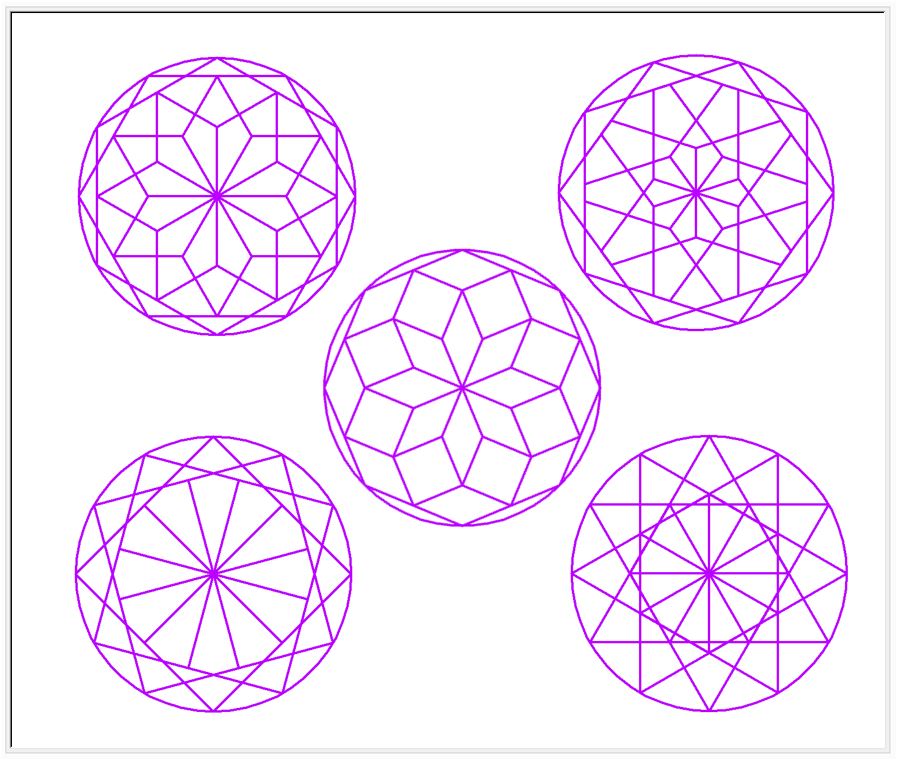
一つの円の中に、正多角形を詰めてみました。あまり重ならないように、適度に。この “適度に” は難しいことですが。亀さんが円内を動き回って、正多角形を詰めてくれました。
下の図、ちょと見て、正 ”何” 角形 からできているかわかりますでしょうか。
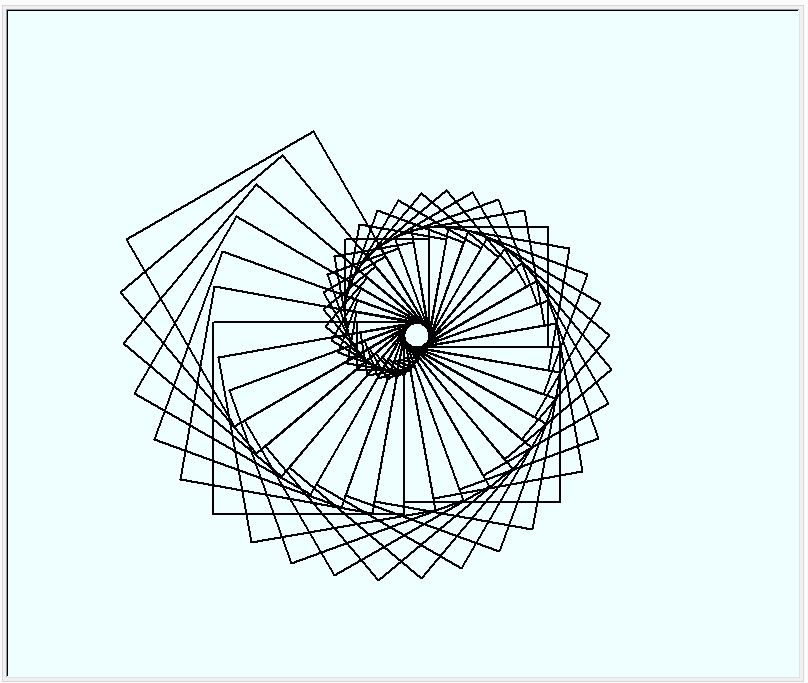
単純な形でも、すこしづつ移動させながら重ねて描くと、なかなか面白い図形になります。下図は、正四角形と正三角形を、中心点で回転させながら、徐々に辺を長くしたものです。回転軸は図形の中心点です
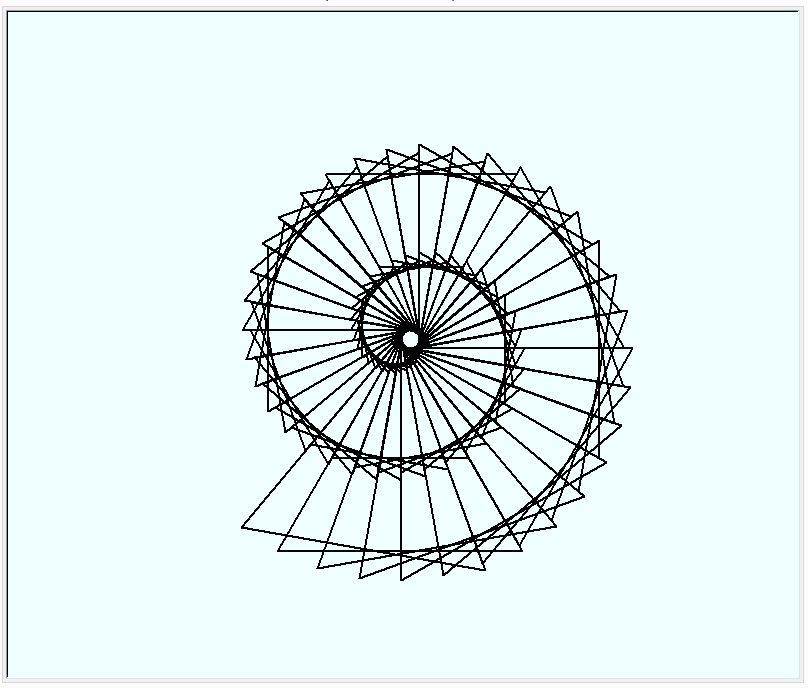
次も、正四角形と正三角形を回転させながら、回転ごとに、辺を伸ばしていきました。先の図形と異なり、こちらは、回転軸を中心ではなく、正四角形/三角形の一隅にとりました。描きあがった図形は、巻貝、あるいは、アンモナイトの形状に見えます。
回転させる形や回転に伴うパラメーターを変更しては、亀が描く図形が変化していく様子をながめています。なかなか、楽しいものです。
Pythonの亀グラフィックス(3)
2019 09 05(art19-0168)
Pythonの亀グラフィックスを楽しんでいます。
亀を動かす指令に、goto()があります。これは、「亀さん、(X、Y) 座標へ移動して」と言うものです。画面上に直交する X軸と Y軸をとると、画面上の任意の点は X値と Y値からなる(X、Y)座標であらわすことができます。亀さんへの指令 goto(X, Y)を使いますと、画面上の任意の点へ亀を移動させることができます。もちろん、けなげな亀は移動しながら線を描いてくれます。
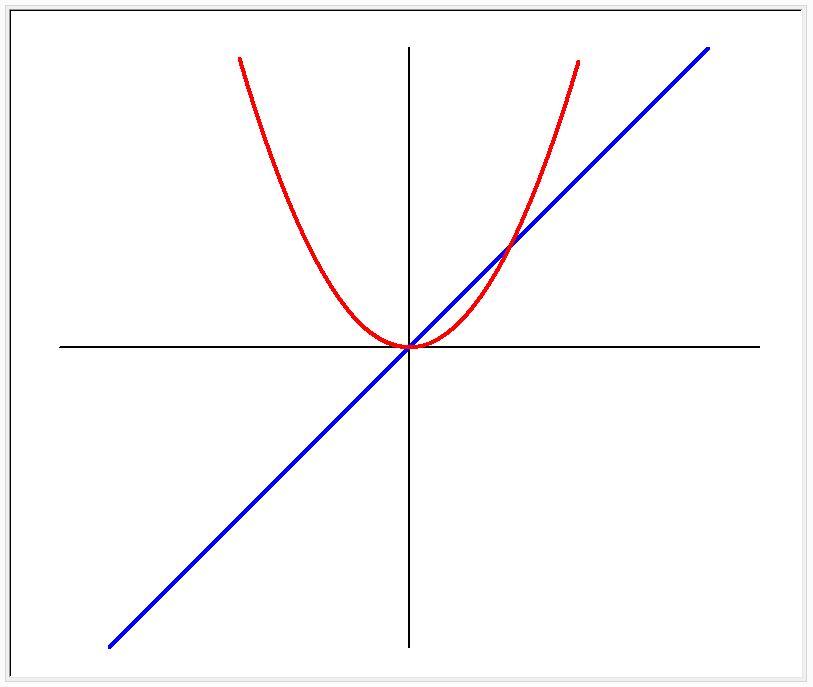
Y値がXによって決定される関数、Y = f (X)は、X-Y座標上に描くことができます。中学で学習した1次関数(Y = X)と2次関数(Y = X^2)は、Xを横軸に、Yを縦軸にとると、下図のように描けます。XとY軸の交点は、(0、0)です。(注:2次関数は、図面からはみ出ないようにY値を1/100に縮小しています)
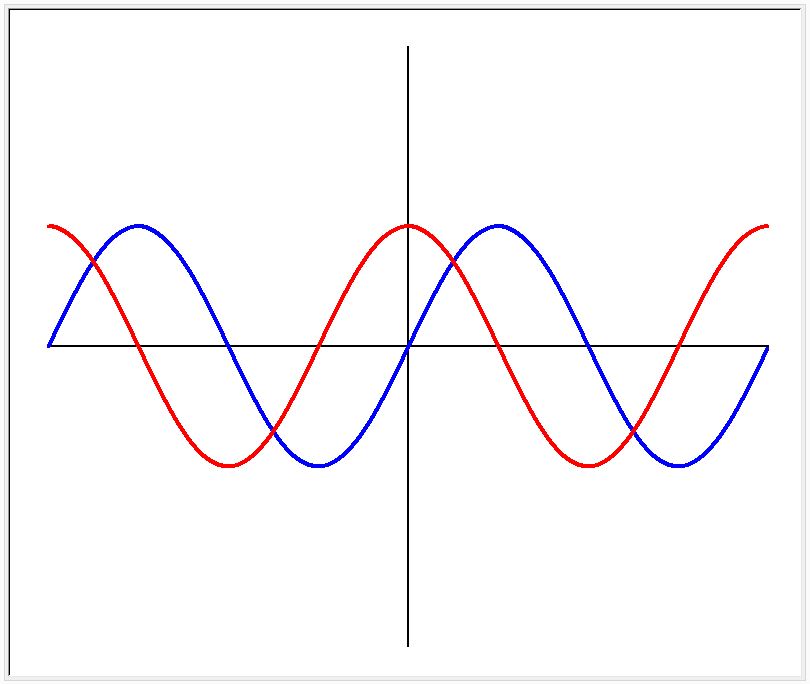
同様に、三角関数、サイン(sin) とコサイン(cos)は、X,Yの関数式、Y = Asin (X) と Y = Acos (X) であらわせます。Xが (-360度) から (360度) へ変化するときの、サイン、コサインの値を(X、Y)座標にプロットすると、下図のような波形になります。青がサインで、赤がコサインです。位相が90度ずれていることが分かります。
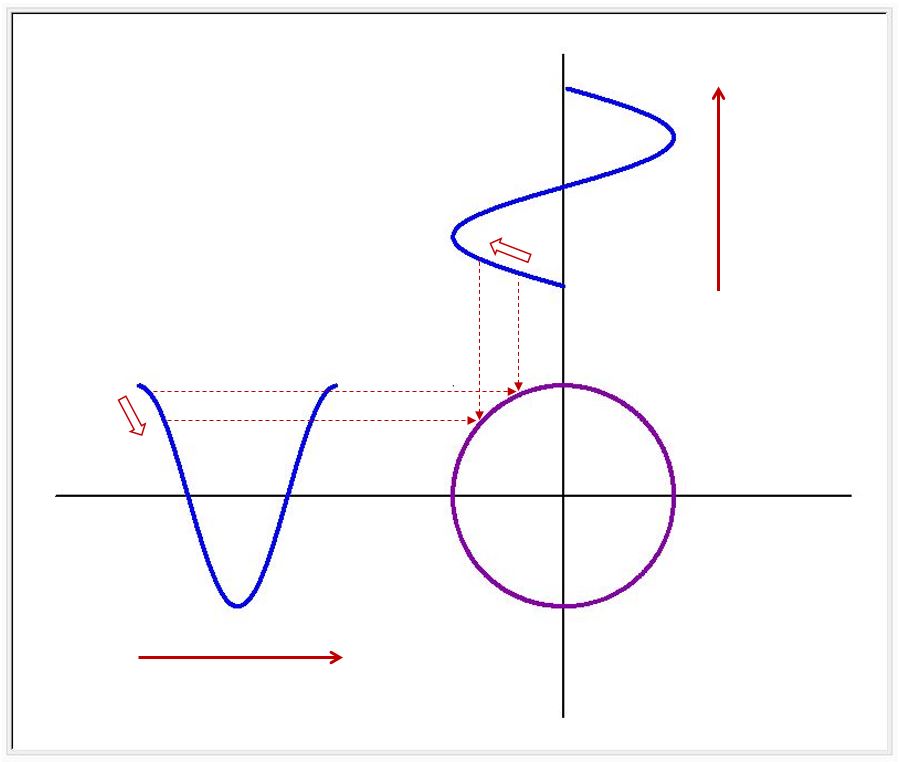
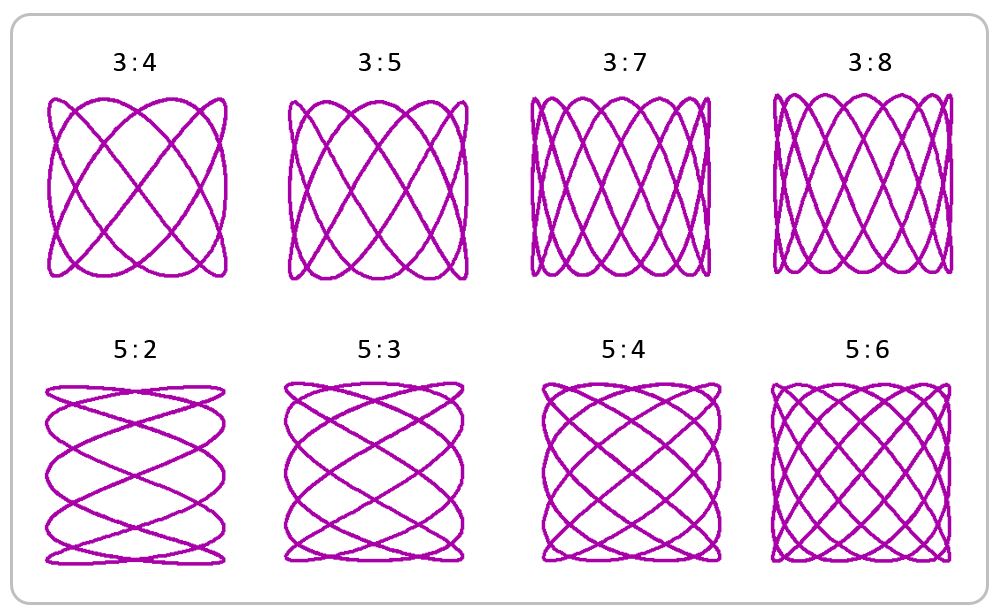
2つのサイン、コサインのような波を直角に合わせるとリサージュ波形ができます。波の大きさが同じ場合、両波の周波数(振動数)が同じであれば、リサージュ波形は円になります。(2つの波形の位相のずれによって、円形―楕円形―直線の間で変化します。位相が90度、270度ずれている場合は円形で、0度、180度ずれていると直線になります)。両波の周波数(振動数)が異なっている場合は、少し複雑な波形となります。下図は、周波数(振動数)の比が、1:1 と 1:3 の場合に形成されるリサージュ波形です。
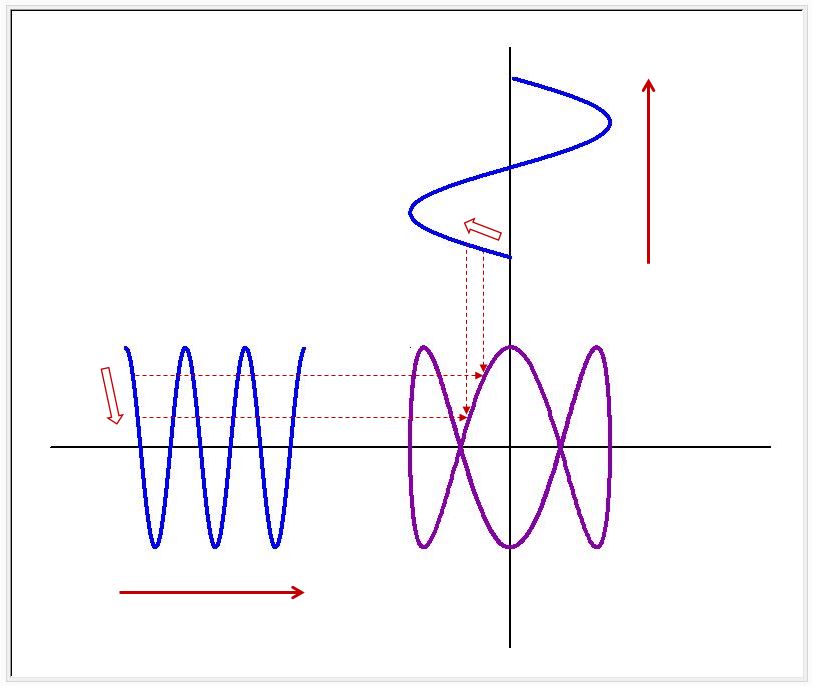
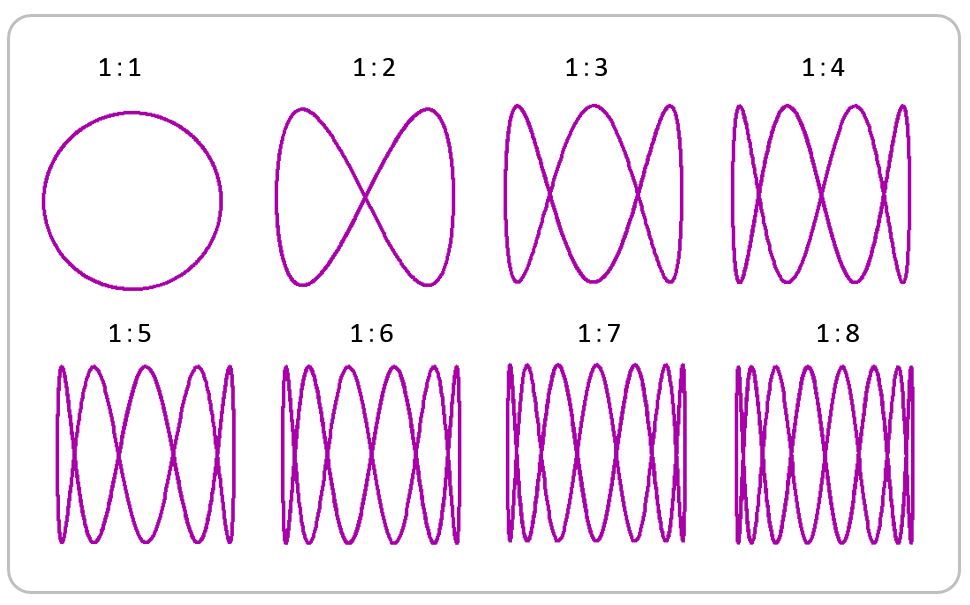
リサージュ波形は、X,Yが時間 t の関数 X (t) と Y (t) としてあらわすことができます。数式は、X = A sin (at + δ) Y = B sin (bt)です。ここで、A、Bは波の大きさ、a:b は周波数比、δ は位相差です。下図に、周波数比を 1:1 から 1:8 へと変化させた時のリサージュ波形を示します。横方向の山の数は1ですが、縦方向の山の数が 1,2,3,4,5,6,7,8 と変化していくことがわかります。
一方、周波数比が複雑(整数倍の関係から外れる)になると、波形も複雑になります。しかし、横山と縦山の数は、3つと4つ、3つと5つなどと、周波数比の 3:4 と 3:5 などに対応していることがわかります(下図)。
このように、両波の周波数比の違いによって、リサージュ波形が異なります。このリサージュ波形の特性を周波数の測定に応用したものが、オシロスコープです。周波数を測定したい波に、周波数が分かっている波を、直交させてリサージュ波形を描きます。リサージュ波形をみながら周波数が分かっている波の周波数を変えていき、リサージュ波形が複雑な波形から単純なものになり、そして円形/直線になるところを探します。この時の周波数が、測定したい波の周波数となります。
米子高専の電気科に在籍していたとき電気測定器機実習がありました。オシロスコープのブラウン管に映しだされる青緑の蛍光色の波形が幾通りにも変化する様は、見ていて飽きないものでした。
Pythonの亀グラフィックス(2)
2019 09 02(art19-0167)
前回、Pythonの亀グラフィックスで描いた図形を紹介しました。円状に並ぶ 24点で、同心円(9個の異なる半径の円からなる)を描かせたものです。なかなか、おもしろい図形になりました。
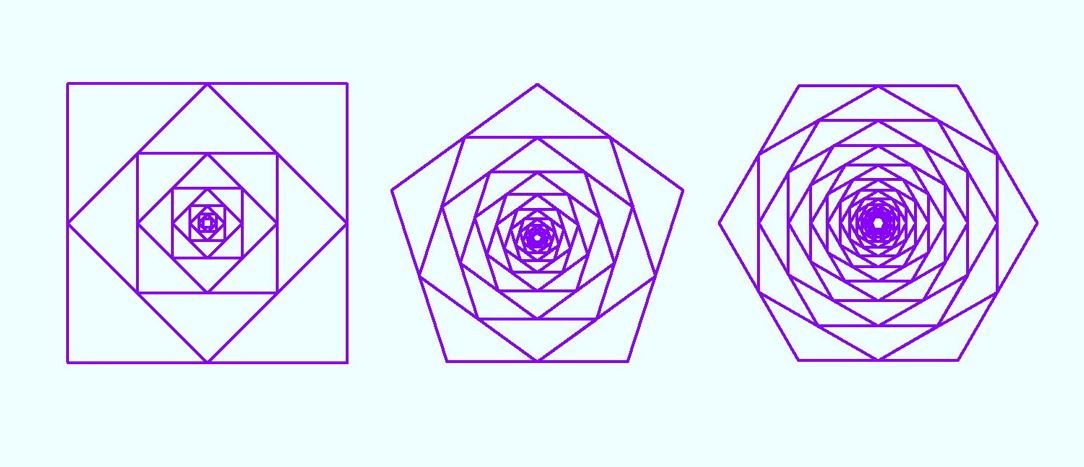
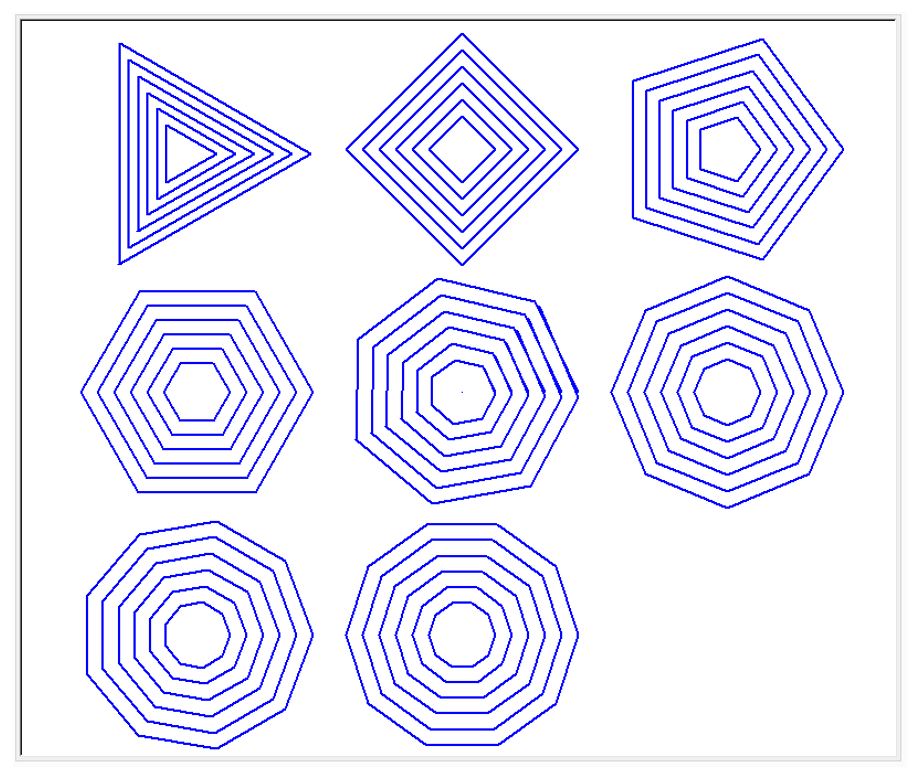
ベースの図形に円を使ったのですが、他の形をつかえばどうなるだろうかと、3 - 10角形を使ってみました。同じ中心をもつ、大きさの異なる正多角形(下図)を、円状に並ぶ 24点に描きました。正多角形の向きは放射線状になるようにしました。
亀さんが、画面上を動き回り、24個の同心の正多角形を描いてくれました。
下図は、正3角形、正4角形、正5角形、そして正6角形をベースにした図形です。
正多角形の角数が多くなる(7 - 10角、下図)と、一見同じような模様が出てきますが、よく見ると微妙に違いがあります。
今回は、正多角形の角数だけを、3 - 10と変化させたのですが、他のパラメーター(例えば、同心形同士の間隔、24点の円状配置の広がりなど)を変えれば、同じ、正多角形でも模様が大きく変わります。逆に言えば、描きたい模様があり、それを描かせるパラメーターを知ることは、大変な作業になりそうです。さらに、完成図から、どのように描いたのかを知るすべはあるのでしょうか。このあたり、機械に解けるのか解けないのか、たいへん興味をそそられます。
それにしても、これらの模様、どこかでみたことがあります。それも、非常に身近なものに。思い出しました、ガラス製の皿型の吸い殻入れの模様です。ガラスのカット模様に似ています。今は、使われることなく2階の物置小部屋に収まっています。
【戻る】





















m_triangle.jpg)
_quare.jpg)
.jpg)
.jpg)
.jpg)
.jpg)
.jpg)
.jpg)